Algorithm Ch8 Sort in linear time

Lower bounds for sorting

• to examine all the input
• All sort lower bound are
• is lower bound for comparison test

Decision Tree

• Abstration of any comparison sort
• Represents comparison made by
  • specific sorting algorithm
  • on input of a given size
• Abstract away conotrol & data movement, etc.
  • counting only comparison

For insertion sort on 3 elements

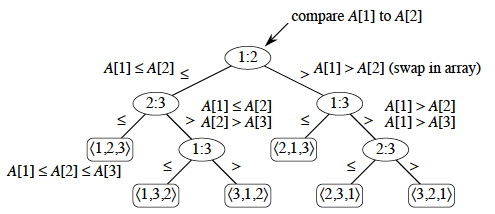* internal node: indices of array elements from their original pos. * leaf: permutation of orders that the algorithm determines * leaf numbers >= n!

For any comparison sort

• 1 tree for each n
• view the tree: like algorithm splits in two at each node, base on the inf. is has determined up to that point
• tree models all possible execution tracs

length of the longest path from root to leaf

depends on the algorithm

• Insertion Sort
• Merge Sort

lemma:

any binary tree of height h has <= leaves

• l = # of leaves
• h = height
• l <=

The.

any decision tree that sorts n ele. has height

• Proof.
  l >= n!
  By lemma,
  Take logs, h >= lg(n!)
  Use Stirling;s appor.,
  $h >= lg(n/e)^n = nlg(n/e) = nlgn - nlge = \Omega(n,lg,n)

Corollary

Heapsort, merge sort are asymptotically optimal comparison sort(最優排序)

Sorting in linear time

Counting sort

Depends on a key assumption: numbers <- {0, 1, …, k}

• Input: A[1…n], where A[j] <- {0, …, k} for all j
• Output: B[1…n], B should be already allocated
• Auxiliary Storage: C[0…k]

pseudo code

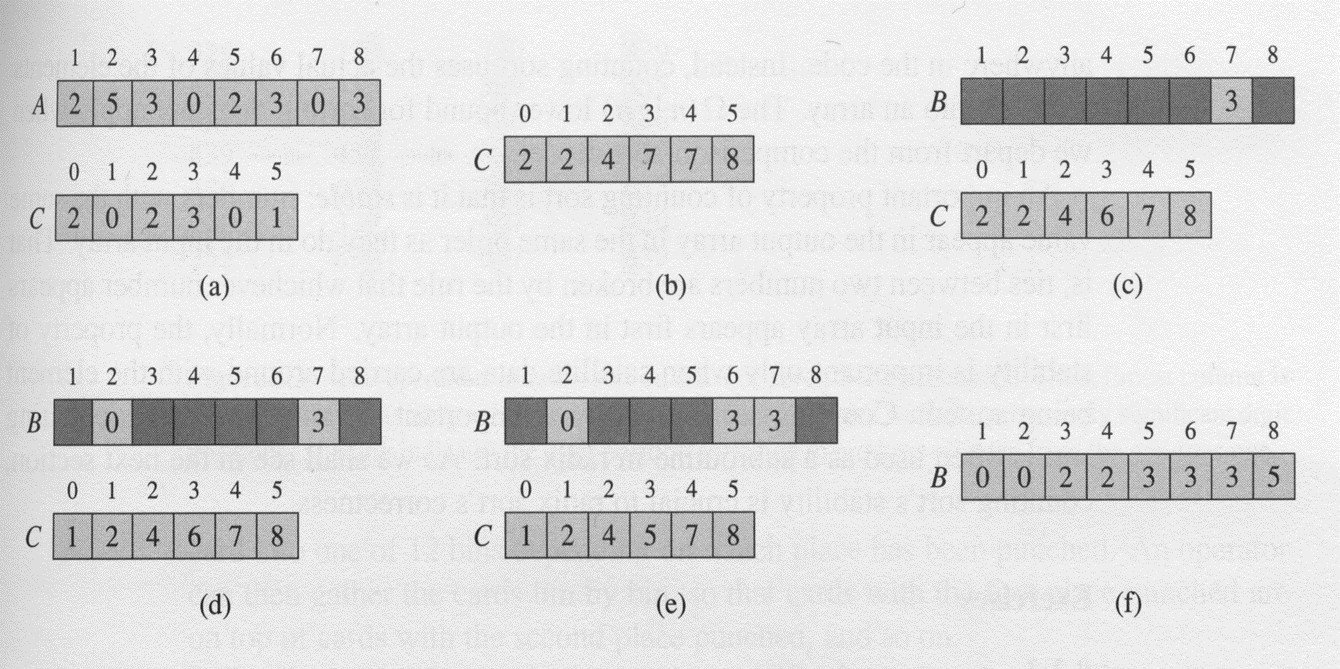
property

• stable because of how the last loop works
  • keys with same value appear in same order

Analysis

, which is if k =
Is k practical?

• 32-bit? No
• 16-bit? probably not
• 8-bit? Maybe, depending on n
• 4-bit? Probably
• Counting sort used in radix sort

Radix Sort

Sort least significant digits first
To sort d digits:

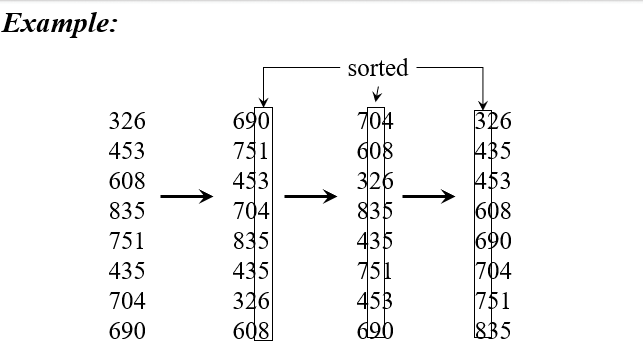
Correctness

Assume digits 1, 2, …, i-1 is already sorted
for digit:

• if two digit are different -> by counting sort
• if … are equal -> count sort is stable, keep order before

It shows why it’s important to use a stable sort for intermediate sort

Analyse

Assume intermediate sort is counting sort

• per pass (digit in range 0, …, k)
• d pass
• total
• if k = , time =

Break digit

• n words
• b bits per word
• Break into r-bit digits. Have d = [b/r]
• Using counting sort, k = -1
  • EX. 32-bit words, 8-bits digits.
  • b = 32, r = 8, d = [32/8] = 4
  • k = - 1 = 255
• Time =

How to choose r?

Balance and n + , choosing r lg n

give us =

• if r < lg n
  • >
  • n + do not improve, keep
• if r > lg n
  • n + gets big
  • Ex. r = 2lg n = =

So, to sort 32-bit numbers, use r = lg = 16 bit, which do 2 passes

Compare

• 1 million () 32-bit int.
• Radix sort: ceil(32/20) = 2 passes
• Merge sort/quick sort: lg n = 20 passes
• each passes in radix sort is really 2
  • one to take census
  • one to move data

why radix can violate ground rule of comparison sort

• using counting sort allows us to gain inf. about key by means other than comparison
• used keys as array indices

Bucket sort

Assume the input is generated by a random process that distributes ee/ uniformly over [0, 1)

Idea:

• Divide [0, 1) into n equal-sized buckets
• Distribute the n input values into the bucket
• sort each bucket
• go through buckets in order, listing ele. in each one

Input: A[1…n], where 0 <= A[i] < 1 for all i
Auxiliary array: B[0…n-1] of linked lists, each list init. empty

Correctness

• Consider A[i], A[j], WLOG, A[i] <= A[j]
• than floor(nA[i]) <= floor(nA[j])
• thus A[i], A[j]
  • in the same bucket, by insertion sort => fixes up
  • other wise, by concatenation in ordere => fixes up

Analyse

• relies on no buckets getting too many values
• All lines of algo. excpt inserting sort take altogether(除了插入排序，其他部分總共需要…)
• Intuitively, if each bucket gets a constant number of ele., it takes time to sort each bucket
  • for all bucket
• except each bucket to have few ele., since the average is 1 ele. per bucket

careful Analyse

Def. a RV.

• = the number of ele. placd in bucket B[i]

Because insertion sort run in quadratic time, bucket sort time is

• T(n) = + $\sum^{n-1}{i=0}O(n{i}^{2})$

Take expectations,

• E[T(n)] = E[ + $\sum^{n-1}{i=0}O(n{i}^{2})\Theta(n)\sum^{n-1}{i=0}E(O(n{i}^{2}))\Theta(n)\sum^{n-1}{i=0}O(E(n{i}^{2}))$

Claim,
= 2 - (1/n) for i = 0, …, n-1

proof of claim,
Def. indicator RV.

• = I{A[j] falls in bucket i}
• Pr{A[j] falls in bucket i} = 1/n
• =

Then,
= = =

= Pr{A[j] do not fall in bucket i} + Pr{A[j] falls in bucket i} = 0(1 - ) + 1 =

for j

• and are independent RV.
• than is = =

Therefore
= + 2 = + = 1 + = 1+1- = 2-

thus
E[T(n)] = = + =

End up

• not a comparison sort
• probabilistic analysis
• different from a randomized algo., where we use randomization to impose a distribution
• With bucket sort, if the input isn’t drawn from a uniform distribution on [0,1), all bets are off (performance-wise, but the algorithm is still correct).